Introduction
The Finite Element Method (FEM) is a powerful numerical technique used to solve complex engineering and physical problems. It has become an indispensable tool in various fields, including structural analysis, heat transfer, fluid dynamics, electromagnetism, and biomechanics. The method's versatility and robustness make it applicable to a wide range of real-world problems, from designing aircraft and automobiles to simulating the human body's response to medical treatments. This article delves into the Finite Element Method from an applications perspective, exploring its fundamental principles, key steps, and diverse applications across different industries.
In case you are interested check out YouTube channel or published research
Fundamental Principles of the Finite Element Method
1. Discretization
The core idea behind the Finite Element Method is the discretization of a continuous domain into a finite number of smaller, simpler sub-domains called elements. These elements are interconnected at specific points known as nodes. The process of breaking down a complex problem into smaller, manageable parts is known as meshing. The quality of the mesh, including the size and shape of the elements, significantly impacts the accuracy and efficiency of the FEM solution.
2. Approximation
if you need any help reach out 😊
Once the domain is discretized, the next step is to approximate the solution within each element. This is typically done using interpolation functions, also known as shape functions, which describe how the solution varies within an element based on the values at the nodes. The choice of shape functions depends on the type of problem being solved and the desired accuracy.
3. Assembly
After approximating the solution within each element, the next step is to assemble the global system of equations that represents the entire domain. This involves combining the contributions from all elements and applying boundary conditions and constraints. The resulting system of equations is often large and sparse, requiring efficient numerical methods to solve.
4. Solution
The final step in the FEM process is to solve the global system of equations to obtain the nodal values of the solution. This can be done using direct methods, such as Gaussian elimination, or iterative methods, such as the Conjugate Gradient method. Once the nodal values are known, the solution within each element can be reconstructed using the shape functions.
Key Steps in the Finite Element Method
1. Problem Definition
The first step in applying the Finite Element Method is to clearly define the problem. This includes specifying the geometry, material properties, boundary conditions, and loading conditions. The problem definition also involves selecting the appropriate type of analysis, such as static, dynamic, linear, or nonlinear.
2. Preprocessing
Preprocessing involves creating a finite element model of the problem. This includes generating the mesh, defining material properties, applying boundary conditions, and specifying loads. Preprocessing is a critical step that requires careful attention to detail to ensure the accuracy and reliability of the results.
3. Solution
The solution phase involves solving the global system of equations to obtain the nodal values of the solution. This step is typically performed using specialized software that implements efficient numerical algorithms. The solution phase may also involve iterative processes, such as Newton-Raphson iterations for nonlinear problems.
4. Postprocessing
Postprocessing involves analyzing and visualizing the results obtained from the solution phase. This includes calculating derived quantities, such as stresses, strains, and heat fluxes, and generating plots, contours, and animations to help interpret the results. Postprocessing is essential for understanding the behavior of the system and making informed design decisions.
Applications of the Finite Element Method
1. Structural Analysis
One of the most common applications of the Finite Element Method is in structural analysis. FEM is used to predict the response of structures to various loads, including static, dynamic, and thermal loads. This includes analyzing the stress, strain, deformation, and failure of structures under different conditions.
a. Aerospace Engineering
In aerospace engineering, FEM is used to design and analyze aircraft and spacecraft structures. This includes predicting the structural response to aerodynamic loads, thermal loads, and vibrations. FEM is also used to optimize the design of lightweight and high-strength materials, such as composites, to improve fuel efficiency and performance.
b. Civil Engineering
In civil engineering, FEM is used to analyze the behavior of buildings, bridges, dams, and other infrastructure under various loads, including wind, earthquakes, and traffic. FEM is also used to assess the structural integrity of existing structures and to design retrofitting solutions to improve their safety and durability.
c. Automotive Engineering
In automotive engineering, FEM is used to design and analyze vehicle components, such as chassis, suspension systems, and body panels. This includes predicting the structural response to impact loads, vibrations, and thermal loads. FEM is also used to optimize the design of lightweight materials, such as aluminum and carbon fiber, to improve fuel efficiency and reduce emissions.
2. Heat Transfer Analysis
The Finite Element Method is widely used in heat transfer analysis to predict the temperature distribution and heat flux in solid and fluid domains. This includes analyzing conduction, convection, and radiation heat transfer in various applications.
a. Electronics Cooling
In electronics cooling, FEM is used to design and optimize heat sinks, thermal interface materials, and cooling systems to dissipate heat generated by electronic components. This includes predicting the temperature distribution and heat flux in printed circuit boards (PCBs), integrated circuits (ICs), and other electronic devices.
b. Energy Systems
In energy systems, FEM is used to analyze the thermal performance of power plants, heat exchangers, and renewable energy systems. This includes predicting the temperature distribution and heat flux in boilers, turbines, and solar panels. FEM is also used to optimize the design of thermal energy storage systems to improve energy efficiency and reduce costs.
c. Manufacturing Processes
In manufacturing processes, FEM is used to analyze the thermal behavior of materials during processes such as casting, welding, and heat treatment. This includes predicting the temperature distribution and heat flux in molds, welds, and heat-treated components. FEM is also used to optimize the design of manufacturing processes to improve product quality and reduce production costs.
3. Fluid Dynamics Analysis
The Finite Element Method is also used in fluid dynamics analysis to predict the flow of fluids, including liquids and gases, in various applications. This includes analyzing laminar and turbulent flow, compressible and incompressible flow, and multiphase flow.
a. Aerospace Engineering
In aerospace engineering, FEM is used to analyze the aerodynamic performance of aircraft and spacecraft. This includes predicting the flow of air around wings, fuselages, and control surfaces. FEM is also used to optimize the design of aerodynamic components to improve lift, drag, and stability.
b. Automotive Engineering
In automotive engineering, FEM is used to analyze the flow of air around vehicles to improve aerodynamic performance and reduce drag. This includes predicting the flow of air around car bodies, spoilers, and underbody panels. FEM is also used to optimize the design of cooling systems to improve engine performance and reduce emissions.
c. Biomedical Engineering
In biomedical engineering, FEM is used to analyze the flow of blood in arteries, veins, and artificial blood vessels. This includes predicting the flow of blood in healthy and diseased vessels, as well as in stents and grafts. FEM is also used to optimize the design of medical devices, such as heart valves and catheters, to improve their performance and reduce the risk of complications.
4. Electromagnetic Analysis
The Finite Element Method is used in electromagnetic analysis to predict the behavior of electric and magnetic fields in various applications. This includes analyzing static and dynamic electromagnetic fields, as well as the interaction between electromagnetic fields and materials.
a. Electrical Engineering
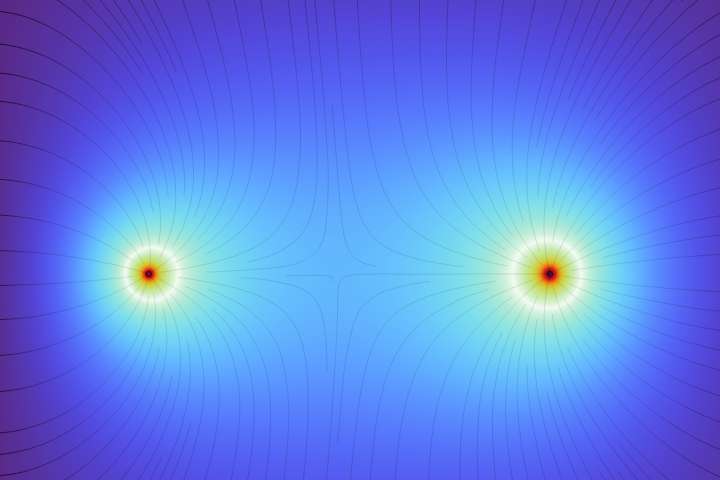
In electrical engineering, FEM is used to design and analyze electrical machines, such as motors, generators, and transformers. This includes predicting the distribution of electric and magnetic fields in the core, windings, and air gaps of electrical machines. FEM is also used to optimize the design of electrical machines to improve efficiency, reduce losses, and increase power density.
b. Electronics
In electronics, FEM is used to analyze the behavior of electromagnetic fields in printed circuit boards (PCBs), integrated circuits (ICs), and other electronic components. This includes predicting the distribution of electric and magnetic fields in signal traces, power planes, and vias. FEM is also used to optimize the design of electronic components to reduce electromagnetic interference (EMI) and improve signal integrity.
c. Telecommunications
In telecommunications, FEM is used to design and analyze antennas, waveguides, and other communication devices. This includes predicting the distribution of electric and magnetic fields in antennas, as well as the propagation of electromagnetic waves in waveguides and transmission lines. FEM is also used to optimize the design of communication devices to improve performance, reduce losses, and increase bandwidth.
5. Biomechanics
The Finite Element Method is widely used in biomechanics to analyze the mechanical behavior of biological tissues and organs. This includes predicting the stress, strain, and deformation of bones, muscles, and soft tissues under various loads and conditions.
a. Orthopedics
In orthopedics, FEM is used to analyze the mechanical behavior of bones and joints under different loading conditions. This includes predicting the stress and strain distribution in bones, as well as the deformation of joints during movement. FEM is also used to optimize the design of orthopedic implants, such as hip and knee replacements, to improve their performance and reduce the risk of failure.
b. Cardiovascular Engineering
In cardiovascular engineering, FEM is used to analyze the mechanical behavior of blood vessels and the heart under different loading conditions. This includes predicting the stress and strain distribution in blood vessels, as well as the deformation of the heart during the cardiac cycle. FEM is also used to optimize the design of cardiovascular devices, such as stents and heart valves, to improve their performance and reduce the risk of complications.
c. Tissue Engineering
In tissue engineering, FEM is used to analyze the mechanical behavior of engineered tissues and scaffolds under different loading conditions. This includes predicting the stress and strain distribution in engineered tissues, as well as the deformation of scaffolds during cell growth and tissue formation. FEM is also used to optimize the design of tissue engineering scaffolds to improve their mechanical properties and promote tissue regeneration.
Conclusion
The Finite Element Method is a versatile and powerful numerical technique that has revolutionized the way engineers and scientists solve complex problems in various fields. From structural analysis and heat transfer to fluid dynamics, electromagnetism, and biomechanics, FEM has become an indispensable tool for predicting the behavior of systems and optimizing their design. The method's ability to break down complex problems into smaller, manageable parts and approximate the solution within each element has made it applicable to a wide range of real-world problems. As computational power continues to increase and software tools become more sophisticated, the applications of the Finite Element Method are expected to expand even further, enabling new discoveries and innovations in engineering and science.
Need suggestions to choose? you can book a meeting here and click on let's talk.
you can contact us (bkacademy.in@gmail.com)
rested to Learn Engineering modelling? Check our Courses?
