COMSOL PDE interface – Equation-based modeling

PDE equation-based simulation in COMSOL Multiphysics (comsol pde interface): An equation with two or more independent variables, an unknown function that depends on those variables, and partial derivatives of the unknown function with respect to the independent variables is known as a partial differential equation (or PDE for short). The largest derivative included determines the partial differential equation's order. A partial differential equation's solution (or a specific solution) is a function that, when substituted into the equation, solves the partial differential equation or, to put it another way, converts it into an identity. If a solution encompasses each unique solution to the equation in question, it is referred to as a generic solution.

Interested to Learn Engineering modelling? Check our Courses?

• Follow writer on LinkedIn

COMSOL PDE interface - Equation-based modeling

In mathematics, a partial differential equation (PDE) is an equation that imposes relations between the various partial derivatives of a multivariable function.

In scientific disciplines that are heavily reliant on mathematics, including physics and engineering, partial differential equations are commonplace. For instance, the Schrödinger equation and the Pauli equation are fundamental to the contemporary scientific knowledge of sound, heat, diffusion, electrostatics, electrodynamics, thermodynamics, fluid dynamics, elasticity, and general relativity, and quantum mechanics. They also result from other purely mathematical issues, such as differential geometry and the calculus of variations. Among other famous uses, they serve as the main means of proving the geometric topological Poincaré conjecture.

Equation-Based Modeling in COMSOL Multiphysics

You may design your own model definitions based on mathematical equations and directly enter them into the software’s graphical user interface using equation-based modeling, which is a key component of COMSOL Multiphysics (GUI).

With the use of these skills, you may fully customize your model to meet your needs and add complexity as you see fit. A built-in interpreter is used by COMSOL Multiphysics to give this flexibility by interpreting equations, expressions, and other mathematical descriptions before creating a model. Additionally, you may create your own physical interfaces using tools like the Physics Builder or whole new user interfaces using the Application Builder.

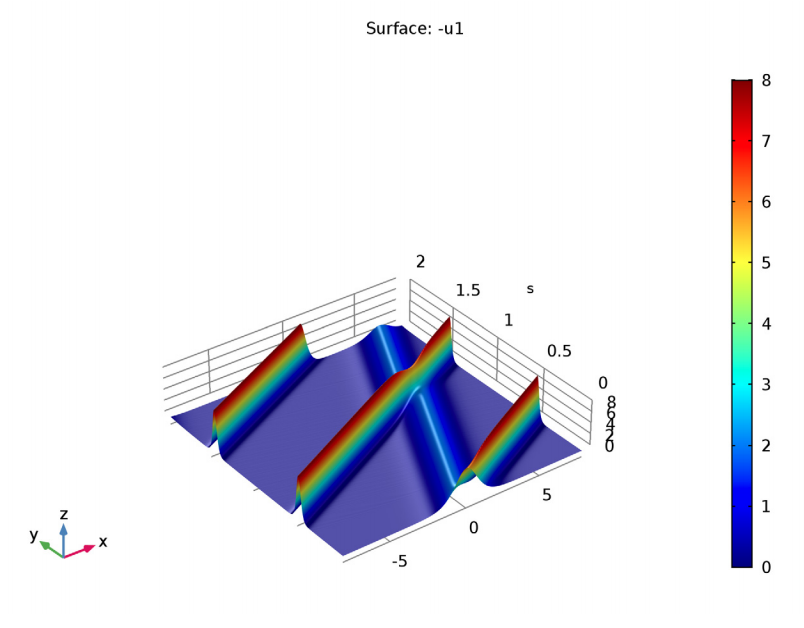
Using this functionality, you can work with:

• Partial differential equations (PDEs)
• Ordinary differential equations (ODEs)
• Algebraic equations
• Differential algebraic equations (DAEs)
• Arbitrary Lagrangian-Eulerian (ALE) methods
• Curvilinear coordinate computation
• Sensitivity analysis

Free tutorial on equation modeling